流密码
\1. 一个东西是不是随机的与长什么模样无关,即使是一串0或者一串1他也有可能是随机的。一个随机的东西符合两点,①它的每一个比特是等概率产生的,即产生每一个比特的概率都是1/2,②任何一个比特的产生与其它比特的产生都是相互独立的。随机与产生的方式有关,与产生的结果无关。
\2. 第一个给“安全”①正式下定义的是香农,他也②提出了完善保密性,并证明了一次一密OTP能够达到完善保密性,③给出了香农定理,提出若一个体制能够达到完善保密性,它就一定要求密钥的长度不能小于明文的长度。一次一密它虽然能达到完善保密性,但并不实用。
\3. 考虑安全性应考虑两个方面,①攻击者能发动什么样的攻击,②攻击者的目标是什么。
\4. 完善保密性是在唯密文攻击下的概念,目标是给了两个明文,区分密文里包含的是哪一个明文。
\5. 虽然一次一密不实用,但它加解密都十分容易只要做一个异或就可以了,人们想既保留优点又实用,因此提出流密码。
\6. 想要实用,需要一个短的密钥去加密明文,又要达到完善保密性,这与香农定理冲突,因此,需要对“安全”重新下定义。
\7. 一次一密的密文没有泄露明文的任何一个信息。为了实用,人们提出计算上安全的概念,即在计算资源有限的情况下,允许密文泄露一些明文信息,只要泄露的信息在计算资源有限的条件下对破译密文的帮助可忽略即可。
\8. 语义安全模型下,攻击者只能询问挑战者一次m0或m1,并且m0和m1的长度相等,挑战者返回密文,在这个条件下攻击者区分密文对应的是m0还是m1。
\9. PRG,给它一个很短的种子,它能产生一个很长的输出,与明文进行异或。
\10. 一个PRG必须满足不可预测性。
\11. PRG的安全性和流密码的安全性是两回事,PRG的安全性要求它的输出与真随机的输出必须是不可区分的,流密码的安全性要求能够达到语义安全性。
\12. “PRG具有不可预测性”与“PRG的输出与真随机的输出不可区分,即PRG是安全的”是等价的,只不过探讨的角度不同。
\13. PRG的输出是可以截断的,截取PRG中的一段,它与等长的真随机是不可区分的。
\14. 使用流密码时,密钥不能重复使用。
\15. 语义安全性是选择明文攻击下的概念,目的是区分两个不同的消息。语义安全性的模型攻击者只能询问一次,CPA下攻击者可以询问多次。
一次一密在唯密文攻击下可以达到完善保密性,在选择明文攻击下可以达到语义安全性。
分组密码
\1. 分组密码输入是一个固定长度的明文分组,输出一般是和明文分组长度相同的分组叫做密文分组(DES:64bits,AES:128bits),分组密码只能处理固定长度的分组信息。
\2. 根据香农的研究,在设计分组密码的时候有两个常用的基本技术,①混乱,②扩散,主要目的是抵抗攻击者对密码系统的统计分析。
\3. 混乱,经常用代换(S盒)的技术实现;扩散,通常用置换(P盒)的技术实现。
\4. 绝大多数的分组密码都是通过迭代技术构造的,迭代技术是一轮一轮的,每一轮都会有一个密钥(轮密钥or子密钥),每一轮也会有一个函数(轮函数),把上一轮的输出作为输入,最后一轮的输出就是密文,第一轮的输入就是明文,轮密钥是由一个密钥扩展来的,扩展的过程会用一个密钥扩展函数把输入的密钥进行一些变换产生每一轮的子密钥。密钥长度不同,轮数不同。(DES 16轮,AES 10轮)
\5. DES的核心是Feistel网络,Feistel网络由Feistel置换组合在一起,DES的每一轮都是一个Feistel置换,16轮置换构成Feistel网络,不论Feistel网络的f是不是可逆的,最终组合在一起都是可以置换的。(搞懂Feistel网络为什么是可逆的)
\6. DES明文长度,密文长度,密钥长度都是64bits,密钥虽然是64bits,但有8bits在转换成子密钥时是不用的,因此有效密钥长度只有56bits。
\7. 目前,没有一个实用的攻击对DES有效,不用DES而用AES是因为DES的密钥长度太短,穷举就可以攻破。
\8. AES使用SPN网络,S盒和P盒交替使用。
\9. 伪随机函数PRF和伪随机置换PRP是用来研究分组密码安全性的,证明时用它们代替分组密码。
\10. 随机函数是指在一个空间有一大堆函数,我们随机挑选一个出来就叫随机函数,不论这个函数的输出怎样,只要是从这个空间随机选择出来的就叫随机函数。是不是随机函数与函数的输出结果无关,与选择的方式有关。
\11. 伪随机置换与伪随机函数类似,是从所有的置换空间随机选择一个出来。
\12. PRP是PRF的一个特例。
\13. 一个PRP就是一个PRF,但一个安全的PRP未必就是一个安全的PRF。
\14. PRF安全引理,只有当分组的长度足够大的时候,一个安全的PRP才是一个安全的PRF。
分组密码的工作模式
\1. ECB模式(电子密码本模式),是一种不安全的模式,不是语义安全的,简单地把明文分成一组一组,用分组密码进行加密,两个相同的明文分组加密后的密文分组相同,当攻击者看到两个相同的密文,虽然不知道明文的内容,但知道对应的明文也相同。
\2. ECB不是语义安全的。
\3. CTR(确定的计数器模式),用PRF构造PRG,可并行。
\4. CPA安全性(选择明文攻击下的语义安全性),攻击者发送多次询问,获得多次对应的密文,即密钥可重复使用。在语义安全性的模型里攻击者只能发送一次询问,获得一次密文,即密钥只用一次。
\5. 凡是确定的加密方案(DES、AES),一定不是CPA安全的。因为给定相同的明文,加密的结果总是相同,但是是语义安全的,因为语义安全刻画的是密钥使用一次。
\6. 一个加密体制如果不是语义安全的,那它也一定不是CPA安全的。
\7. CPA安全性改造思路:加密相同的明文,输出不同的密文。
\8. 改造方法:①随机化加密。选择一个随机数,用密钥和随机数一起加密明文。导致密文必然会比明文要长,密文里不仅包含明文信息,还包含了随机数信息。②nonce-based加密。每加密一个明文就换一个新的nonce(新鲜值),nonce可以作为加密算法的输入,保证加密明文nonce不能重复,除非换一个新的密钥,即(k,n)这个组合不重复使用。
\9. nonce的选择方法:①计数器方式。初始为0,每次加1。如果发送者和接收者保持相同状态,则nonce无需发送。②随机数方式。随机数需与密文一起发送。
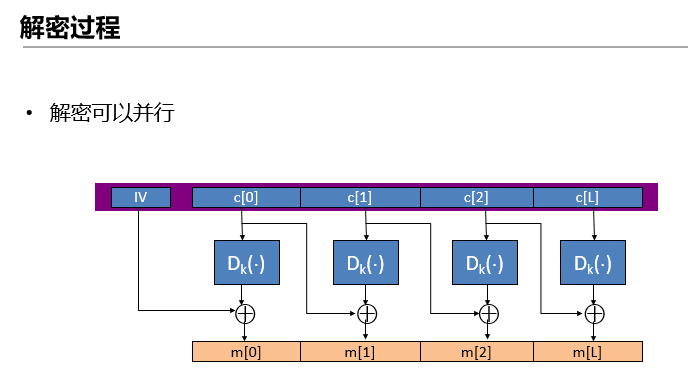
\10. CBC模式(密码分组链接模式)和CTR模式(计数器模式)都能够证明在CPA安全性下是安全的,使用时密钥可以重用。
\11. CBC模式是一种级联的形式,整个加密过程是一个串行的过程,解密可以并行。在加密下一个明文时需要用到前一个密文分组,与当前的明文分组进行异或,再加密。为了隐藏第一个明文的信息,在加密时需要一个初始向量与第一个明文分组进行异或,初始向量在发送给接收者时不需要加密,以明文的形式和密文一起发送给接收者。
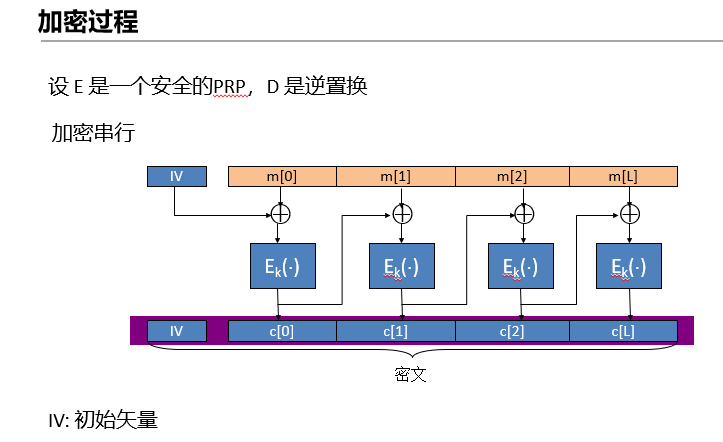
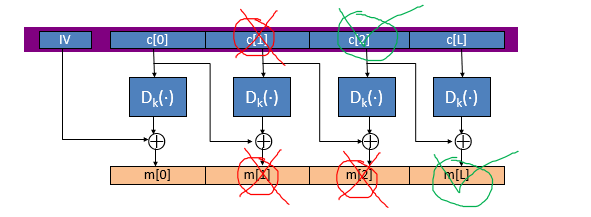
\12. CBC模式中差错传播,单个密文分组在传输或存储过程中发生错误,会影响该分组和后面一个分组的解密。只要后面的分组没发生错误,便不会影响后续分组的解密。
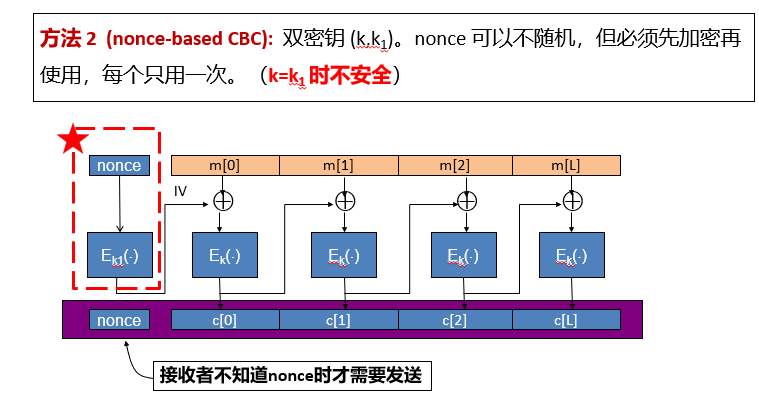
\13. CBC模式中初始向量IV的选择:①取随机数(不能是可预测的,即从上一个IV可预测下一个IV),与密文一起发送。如果IV可预测,则不是CPA安全的。②用nonce作为IV,若nonce随机,则与前面随机数取IV相同,若nonce不随机,可预测,则使用前必须对其进行一次加密,使用双密钥,其中一个密钥用来加密IV,另外一个密钥用在CBC链条里。使用nonce的好处是双方都知道下一个nonce,不需要再发送。
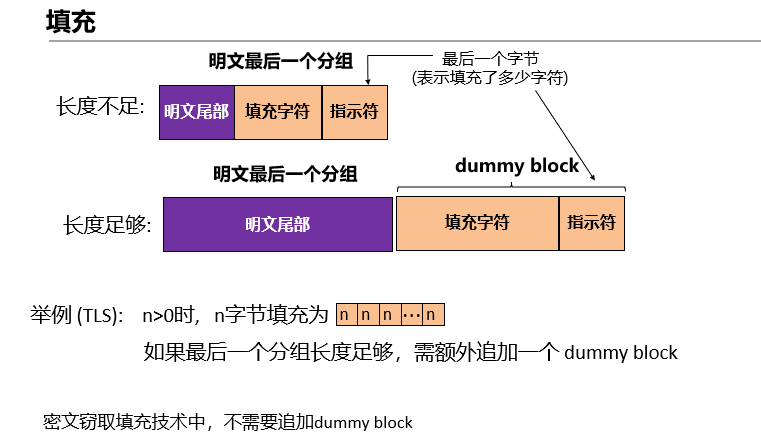
\14. CBC模式中,若分组后最后一个分组的长度不够,则需要进行填充。若明文分组的长度是分组长度的整数倍,依然需要填充,需要额外追加一个完整的分组(dummy block),接收者就会知道不管长度够不够都有填充,若长度不够时填充,整数倍不填充,接收者不知道是否填充,可能会导致解密失败。注:密文窃取填充技术中,不需要追加dummy block。
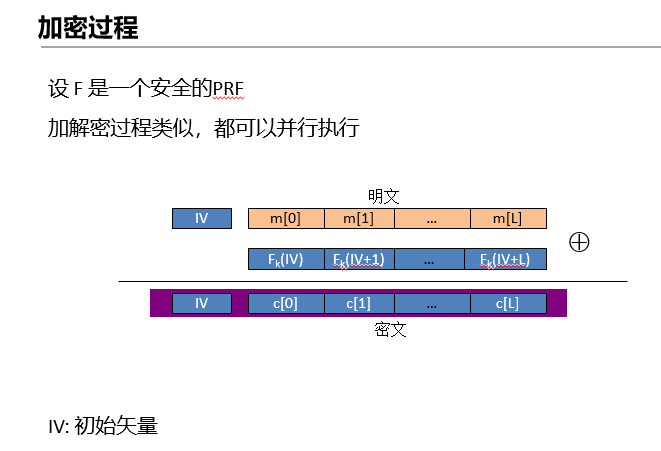
\15. CTR模式,本质上是用一个PRF来构造一个流密码,加解密都可以并行。首先对IV、IV+1、IV+2…进行加密,然后分别与每一个明文分组进行异或,得到密文分组,IV与密文分组一起发送给接收方。CTR不存在差错传播,但不影响其他的分组。
\16. CTR模式中初始向量IV的选择:①取随机数,与密文一起发送。②nonce加密,需要保证Fk(x)不会重复出现。